IntactSDK 1.0.19 User’s Manual¶
Overview¶
This document provides a comprehensive guide to using IntactSDK, a C++ interface for Intact.Simulation. IntactSDK allows users to define geometries, material properties, components, assemblies, and boundary conditions. Users can specify units, create simulation scenarios, execute the simulation, and query the results. The simulations can be run with different solver types and the results can be written to a file for visualization. The document also provides code examples and snippets for each step of the simulation process.
Key features and capabilities
Physics Support
Stress
Modal
Thermal
Geometry Support
Brep: Surface mesh
Level set topology optimization
Prerequisites¶
IntactSDK requires the Intel oneAPI Math Kernel Library. Specifically, at runtime,
it requires libiomp5md.dll, which can be obtained from Intel’s redistributable
downloads.
Installation and usage¶
The IntactSDK package provides headers, in the include/ directory, a static library,
in the lib/ directory, and required third party dependencies, in the bin/ directory.
To use IntactSDK, include the header directory when building your application,
link to the libraries in the lib/ directory, and add the path to the bin/ directory
to the path environment variable so the application can find the required dependencies.
To use the LevelOpt functionality, you must define the symbol INTACT_VDB.
Getting Started¶
The following is simple example, broken down step-by-step, of running a structural simulation. The entire source file and the three required geometry files are available: beam geometry, restraint geometry, load geometry.
Include the Intact header
#include "Intact.hpp"
Create geometry
auto beam_geometry = Intact::MeshModel("beam.stl");
beam_geometry.instance_id = "simple_cantilever";
beam_geometry.refine(0.02); // refine stl for smoother visualization
Create material (material properties are in MKS unit system)
// Create steel material
auto material = std::make_shared<Intact::IsotropicMaterialDescriptor>();
material->density = 7800.0; // kg/m^3
material->poisson_ratio = 0.3;
material->youngs_modulus = 2.1e11; // Pa
Create restraints and loads
// Create a fixed boundary condition at one end of the beam
auto fixed_boundary = std::make_shared<FixedBoundaryDescriptor>();
fixed_boundary->boundary = Intact::MeshModel("restraint.stl");
// Create a pressure load at the free end of the beam
auto pressure_load = std::make_shared<PressureForceDescriptor>();
pressure_load->units = Intact::UnitSystem::MeterKilogramSecond;
pressure_load->magnitude = 1000; // Applying pressure in Pascals
pressure_load->boundary = Intact::MeshModel("load.stl");
Setup simulation and solve
// Setup the simulation scenario descriptor
Intact::LinearElasticScenarioDescriptor scenario;
scenario.boundary_conditions = {fixed_boundary, pressure_load};
scenario.metadata.resolution = 10000;
scenario.metadata.units = Intact::UnitSystem::MeterKilogramSecond;
scenario.materials = {{"Steel", material}};
// Associate the material with the model
auto component = Intact::MaterialDomain(beam_geometry, "Steel", scenario);
Intact::Assembly assembly = {component};
// Create the simulator and solve
Intact::StressSimulator simulator(assembly, scenario);
simulator.solve();
Query result and create output file to visualize
// Query results for stress distribution
Intact::QueryResult results(component);
Intact::FieldQuery stress_query(Intact::FieldType::VonMisesStress);
simulator.sample(stress_query, results);
// Write results to a file (unit system is saved as a metadata in the vtu file)
results.writeVTK("cantilever_beam_results.vtu", Intact::UnitSystem::MeterKilogramSecond);
How To¶
Creating Simulation Input¶
Units¶
The default Unit System is MKS or MeterKilogramSecond. We allow the following customizations:
Specify custom unit for geometry through the
Scenariounit (default MKS)Specify custom unit for loads (default MKS)
Specify custom unit for materials (default MKS)
Unit System Keywords |
Mass |
Force |
Stress |
Length |
Temperature |
Energy |
|---|---|---|---|---|---|---|
MeterKilogramSecond |
kg |
N |
Pa |
m |
K |
J |
CentimeterGramSecond |
g |
dyne |
dyne/cm² |
cm |
K |
dyne·cm |
MillimeterMegagramSecond |
Mg |
N |
MPa |
mm |
K |
mJ |
FootPoundSecond |
slug |
lbf |
lbf/ft² |
ft |
Ra |
lbf·ft |
InchPoundSecond |
lbf s²/in (slinch) |
lbf |
psi |
in |
Ra |
lbf·in |
Geometry¶
Geometry is specified through a Model object.
MeshModel created from a surface mesh can be defined in two ways:
By specifying a
filenameto define mesh from a file (STL, PLY)
auto mesh_geometry = Intact::MeshModel("beam.stl");
mesh_geometry.instance_id = "beam";
By constructing mesh face-by-face
// define an empty mesh
auto mesh_geometry = Intact::MeshModel();
mesh_geometry.instance_id = "fixed_boundary";
// add vertices to the mesh and get the vertex id as output
auto v0 = mesh_geometry.addVertex({0.0, 0.0, 0.0});
auto v1 = mesh_geometry.addVertex({1.0, 0.0, 0.0});
auto v2 = mesh_geometry.addVertex({0.0, 1.0, 0.0});
// add faces defined by the vertex id
mesh_geometry.addFacet(v0, v1, v2);
Meshes can be refined, usually for finer interpolation of results during
visualization, using the MeshModel::refine method with refinement_level
argument. refinement_level is the largest allowed triangle edge as a
ratio of the bounding box diagonal.
// mesh geometry created above is further refined
mesh_geometry.refine(0.02);
Structural Material Properties¶
IsotropicMaterialDescriptorto create an Isotropic material. (Unit system isMeterKilogramSecond)densityis the material densityyoungs_modulusis the elastic moduluspoisson_ratiois the Poisson ratio
auto steel_structural = std::make_shared<Intact::IsotropicMaterialDescriptor>(); // Set the density to 7845 kg/m^3, modulus to 200 GPa and poison ratio to 0.29 steel_structural->density = 7845 steel_structural->youngs_modulus = 200e9 steel_structural->poisson_ratio = 0.29
OrthotropicMaterialDescriptorto create an Orthotropic material. Orthotropic materials are often used to represent composites and wood, where the material properties along one axis are significantly different from the properties along the other axes. (Unit system isMeterKilogramSecond)densityis the material densityExis the elastic modulus in the material’s x-directionEyis the elastic modulus in the material’s y-directionEzis the elastic modulus in the material’s z-directionGxyis the shear modulus in the xy planeGxzis the shear modulus in the xz planeGyzis the shear modulus in the yz planevxyis the poisson ratio in the xy planevxzis the poisson ratio in the xx planevyzis the poisson ratio in the yz planetransformis the optional material transform to arbitrarily rotate the axes along which the material properties are defined. Specified as a list of 9 floating point numbers corresponding to a 3x3 matrix. Note the first 3 floating point numbers corresponds to the first row.
// Create an orthotropic material (Red Pine) auto material = std::make_shared<Intact::OrthotropicMaterialDescriptor>(); material->density = 460.0; // kg/m³ material->Ex = 11.2e9; // Pa material->Ey = 492.8e6; // Pa material->Ez = 985.6e6; // Pa material->Gxy = 907.2e6; // Pa material->Gxz = 1.08e9; // Pa material->Gyz = 123.2e6; // Pa material->vxy = 0.315; material->vxz = 0.347; material->vyz = 0.308; material->transform = {1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 1.0} // transform is optional
Thermal Material Properties¶
ThermalMaterialDescriptorto create a thermal material. (Unit system isMeterKilogramSecond)densityis the material densityconductivityis the conductivity of the materialspecific_heatis the specific heat of the material
auto thermal_material = std::make_shared<Intact::ThermalMaterialDescriptor>(); // Set the density, conductivity, and specific heat of the material thermal_material->density = 2700.0; // kg/m^3 thermal_material->conductivity = 170; // W/(m·K) thermal_material->specific_heat = 500; // J/(kg·K)
Component and Assembly¶
A Component is created as a
MaterialDomainand takes three inputsA
Modelobject (MeshModelspecifically)A material name
A
ScenarioDescriptorobject
auto bar1_structural = Intact::MaterialDomain(mesh_geometry, "Steel", structural_scenario); auto bar2_structural = Intact::MaterialDomain(mesh_geometry, "Red Pine", structural_scenario);
Assembly is a
std::vectorof components that are bonded togetherIntact::Assembly structural_assembly = {bar1_structural, bar2_structural};
Boundary Conditions¶
Restraints
Fixed Boundary A “Fixed Boundary” restraint fixes the selected geometry in all directions.
The fixed boundary only has one input:
the
boundarysurface to be fixed
auto fixed = std::make_shared<Intact::FixedBoundaryDescriptor>(); // Set the geometry "restraint.ply" to be fixed fixed->boundary = Intact::MeshModel("restraint.ply");
Fixed Vector A “Fixed Vector” restraint allows for each direction to be optionally set to a specified displacement value, 0 being fixed and no value (
std::nullopt) being un-restrained. Note that a structural problem must have all three directions restrained somewhere to be valid.A fixed vector has five inputs:
the
boundarysurface to be fixedthe
x_valueto set the displacement for the x-axis direction (optional)the
y_valueto set the displacement for the y-axis direction (optional)the
z_valueto set the displacement for the z-axis direction (optional)the
unitsthat apply to the displacement values
auto fixed_vector = std::make_shared<Intact::FixedVectorDescriptor>(); // Set the geometry "restraint.stl" to be restrained fixed_vector->boundary = Intact::MeshModel("restraint.stl"); // Set the displacements in each direction fixed_vector->x_value = 0.2; // X-direction displacement of 0.2 ft fixed_vector->y_value = std::nullopt; // un-restrained in the Y-direction at this surface fixed_vector->z_value = 0.0; // fixed Z-direction fixed_vector->units = Intact::UnitSystem::FootPoundSecond;
Sliding Restraint A “Sliding Restraint” allows for motion tangential to a specified surface, but fixes motion normal to the specified surface.
A sliding restraint only has one input:
the
boundarysurface for the sliding restraint condition
auto sliding_boundary = std::make_shared<Intact::SlidingBoundaryDescriptor>(); // Set the geometry "restraint.stl" for the sliding restraint condition sliding_boundary->boundary = Intact::MeshModel("restraint.stl");
Structural Loads (
TractionDescriptor)Vector Force
“Vector Force” load is a surface load applied to a face in a specified direction. An example of this load is pressing on the top of a book to push it across a table.
A vector load requires four inputs:
the
boundarysurfaces where the load is appliedthe
directionvector of the forcethe
unitsthat apply to the magnitudethe
magnitudeof the force.
auto load = std::make_shared<Intact::VectorForceDescriptor>(); // Set the geometry "load.stl" the vector load is applied to load->boundary = Intact::MeshModel("load.stl"); // Set the vector load direction to be in the -Z direction with a magnitude of 100 lbf load->direction = {0, 0, -1}; load->units = Intact::UnitSystem::InchPoundSecond; load->magnitude = 100; // lbf
Torque
“Torque” load is a surface load that applies a twisting force around an axis. The direction of the torque is determined using the right-hand rule: using your right hand, point your thumb in the direction of the axis. A positive torque value applies a torque acting in the direction the fingers of your right hand would wrap around the axis. The torque load is applied among the load faces with a distribution that varies linearly from zero at the axis.
A Torque load requires five inputs:
the
boundarysurfaces where the load is appliedthe
axisof rotation about which the torque actsoriginis the starting point of the axis of rotationthe
unitsthat apply to the magnitudemagnitudeof the torque.
auto torque_load = std::make_shared<Intact::TorqueForceDescriptor>(); // Set the geometry "load.stl" the torque load is applied to torque_load->boundary = Intact::MeshModel("load.stl"); // Set the axis of the torque axis torque_load->origin = {10, 1, 1}; torque_load->axis = {1, 0, 0}; // Set the torque to be about the +X (right-hand rule) torque_load->units = Intact::UnitSystem::MeterKilogramSecond; torque_load->magnitude = 10; // Set the torque magnitude to 10 N*m
Pressure
A “Pressure” load is a surface load specified in terms of force per unit area. Positive pressures ‘push’ into the surface, and negative pressures ‘pull’.
A Pressure Load requires three inputs:
the
boundarysurfaces where the load is appliedthe
unitsthat apply to the magnitudethe
magnitudeof the pressure.
auto pressure_load = std::make_shared<Intact::PressureForceDescriptor>(); // Set the geometry "load.stl" the pressure load is applied to pressure_load->boundary = Intact::MeshModel("load.stl"); // Set the pressure magnitude to 10 Pa pressure_load->units = Intact::UnitSystem::MeterKilogramSecond; pressure_load->magnitude = 10;
Bearing Force
A “Bearing Force” is a surface load applied to a (typically) cylindrical face to approximate the effects of a shaft pressing against the side of a hole. The applied force gets converted to a varying pressure distribution on the portion of the face experiencing compressive pressure. The pressure distribution is computed automatically to achieve the specified overall bearing force.
A Bearing Force requires three inputs:
the
boundarysurfaces where the load is appliedthe
directionvector of the bearing forcethe
unitsthat apply to the magnitudethe
magnitudeof the force
auto bearing_load = std::make_shared<Intact::BearingForceDescripto>r(); // Set the geometry "load.stl" the bearing load is applied to bearing_load->boundary = Intact::MeshModel("load.stl"); // Set the loading direction to be in the -Z bearing_load->direction = {0, 0, -1}; // Set the magnitude of the load to 100 N bearing_load->units = Intact::UnitSystem::MeterKilogramSecond; bearing_load->magnitude = 100;
Thermal Loads
Fixed Boundary (Fixed Temperature)
A “Fixed Boundary” load fixes the selected geometry to a specified temperature when the
valueis specified and non-zero.The fixed boundary has three inputs:
the
boundarysurface to be fixedthe
valueof the temperature to fix at the boundary surfacethe
unitsthat apply to the temperature (SI - K, English - Ra)
auto fixed = std::make_shared<Intact::FixedBoundaryDescriptor>(); // Set the geometry "fixed_temp.ply" to set a fixed temperaure of 320 K fixed_boundary->boundary = Intact::MeshModel("fixed_temp.ply"); fixed_boundary->value = 320; // Kelvin // Set the geometry "fixed_temp.ply" to set a fixed temperaure of 500 Rankine fixed_boundary->boundary = Intact::MeshModel("fixed_temp.ply"); fixed_boundary->units = Intact::UnitSystem::InchPoundSecond; fixed_boundary->value = 500; // Rankine
Convection
A “Convection” load specifies the transfer of heat from a surrounding medium.
A thermal convection boundary condition requires three inputs:
the
boundarysurface(s) where the convection is applied.the heat transfer
coefficientthe
environment_temperatureof the surrounding mediumthe
units(default MKS)
// Create an instance of ConvectionDescriptor auto convection = std::make_shared<Intact::ConvectionDescriptor>(); convection->units = Intact::UnitSystem::MeterKilogramSecond; // Set the geometry "face.ply" the convection is applied to convection->boundary = Intact::MeshModel("face.ply"); // Set the heat transfer coefficient to 25 W/m^2K and environment temperature convection->coefficient = 25; // W/m^2K convection->environment_temperature = 300; // Kelvin
Surface Flux
Surface “Thermal or Heat Flux” specifies the heat flow per unit of surface area.
A surface thermal flux requires two inputs:
the
boundarysurface(s) where the flux is applied.the
magnitudeof the heat fluxthe
units(default MKS)
// Create an instance of ConstantFluxDescriptor auto flux = std::make_shared<Intact::ConstantFluxDescriptor>(); flux->units = Intact::UnitSystem::MeterKilogramSecond; // Set the geometry "face.ply" the constant flux is applied to flux->boundary = Intact::MeshModel("face.ply"); // Set the flux magnitude to 500 W/m^2 flux->magnitude = 500; // W/m^2
Body Loads/Internal Conditions
Add body load to the scenario as shown below. (see Scenario Setup section for more details)
scenario.internal_conditions = {rotational_load, gravity_load};
Body Load (Linear Acceleration, Gravity)
Body loads comprise forces that are distributed over a solid volume. They are specified by entering the components of a linear acceleration vector field in which the body is immersed. The material in the body will tend to be pulled in the direction of the acceleration vector.
The inputs to the body load are:
the
directionvector of the acceleration fieldthe
unitsthat apply to the magnitudethe
magnitudeof acceleration
// Example for a "gravity load" auto body_load = std::make_shared<Intact::BodyLoadDescriptor>(); // Set the direction vector to be downward (-Z) body_load->direction = {0, 0, -1}; // Set the magnitude to 9.80655 m/s^2 body_load->units = Intact::UnitSystem::MeterKilogramSecond; body_load->magnitude = 9.80665;
Rotational Load
Rotational body loads simulate the effect of a body rotating around an axis. Two contributions are considered in a rotational body load: angular velocity and angular acceleration. The angular velocity term simulates the centrifugal effects that tend to throw a body’s material away from the axis of rotation. The angular acceleration term simulates the effect of a rotational acceleration field around the axis of rotation. A positive angular acceleration tends to drag the body’s material in the positive rotational direction according to the right-hand rule.
A rotational body load has 4 inputs:
originpoint for the axis of rotationvector defining the
axisof rotationangular_velocity(in radians/sec)angular_acceleration(in radians/sec²)
auto rotational_load = std::make_shared<Intact::RotationalLoadDescriptor>(); // Set the origin at the coordinate system origin rotational_load->origin = {0, 0, 0}; // Set the axis of rotation about the y-axis rotational_load->axis = {0, 1, 0}; // Set angular velocity to 10 rad/s and angular acceleration to 0.5 rad/s^2 rotational_load->angular_velocity = 10; rotational_load->angular_acceleration = 0.5;
Thermal Loads
Constant Heat
A “Constant Heat” or body heat flux load applies uniform heat generation over a specified volume.
Constant heat flux has 2 inputs
the
instance_idof the components which are producing heat fluxthe
magnitudeof the body heat fluxthe
units(default MKS)
auto constant_heat = std::make_shared<Intact::ConstantHeatDescriptor>(); constant_heat->units = Intact::UnitSystem::MeterKilogramSecond; // Set the heat generation to -200,000 W for a beam component constant_heat->instance_id = "beam"; constant_heat->magnitude = -200000.0; // W
Simulation Scenario Setup and Solution¶
Scenario Setup using
ScenarioDescriptorLinear Elasticity scenario is created using
LinearElasticScenarioDescriptor. It takes the following inputs:boundary_conditions, a list of boundary conditionsinternal_conditions, a list of internal conditions (body loads)
Scenario Metadata,
metadata, a set of solver parameters to control the accuracy and speed of the simulation:resolutionis the target number of finite elements. An iterative process determines acell_sizethat achieves approximately the specified number of elements. You can directly specify thecell_sizeinstead ofresolution. Note that decreasingcell_sizecan quickly result in large numbers of finite elements and long solve times.resolutionis recommended for most cases.unitssets the unit of the scenario (geometry and results will be in this unit) for example, a geometry in ‘MKS’ that is 6 m long would be 6 mm long when set to ‘MMS’basis_orderis the type of finite element used. The default is 1, which would be linear elements. 2 is for quadratic elements.solver_typeis the solver type used in the simulation with the following options:MKL_PardisoLDLT(default) is the direct solver and is typically faster for lower resolution (< 200K cells on 32 GB memory), but gets slower and consumes more memory at higher resolutionsAMGCL_amg_rigid_bodyis the iterative solver which is typically faster at high resolution.
Intact::LinearElasticScenarioDescriptor scenario; scenario.materials = {{"Aluminum 6061-T6": material}}; scenario.boundary_conditions = {fixed_boundary, vector_load, torque_load}; scenario.internal_conditions = {body_load}; scenario.metadata.resolution = 10000; scenario.metadata.units = Intact::UnitSystem::MeterKilogramSecond; // Optional settings scenario.metadata.basis_order = 2; // 2 = quadratic elements scenario.metadata.solver_override = Intact::SolverType::AMGCL_amg_rigid_body; // iterative solver
Similarly, Modal scenario is created using
ModalScenarioDescriptorwhich takesboundary_conditions, a list of boundary conditions, as input.The
metadatais the same as for the linear elastic scenario except there is necessary inputmetadata.desired_eigenvaluesthat takes in an integer for the number of eigenvalues.
// Setup the modal simulation scenario Intact::ModalScenarioDescriptor modal_scenario; modal_scenario.materials = {{"Aluminum 6061-T6": material}}; modal_scenario.boundary_conditions = {fixed_boundary}; modal_scenario.metadata.resolution = 10000; modal_scenario.modal_metadata.desired_eigenvalues = 10; // Optional settings modal_scenario.metadata.basis_order = 2; // 2 = quadratic elements modal_scenario.metadata.solver_override = Intact::SolverType::AMGCL_amg_rigid_body; // iterative solver
Similarly, a thermal scenario is created using
StaticThermalScenarioDescriptorwhich takes a list ofboundary_conditionsand a list ofinternal_conditionsas input. Note that thematerialmust be a thermal material for this scenario type.The
metadatais the same as for the linear elastic scenario with additional inputmetadata.environment_temperaturewhich specifies the temperature of the environment.
// Setup the thermal simulation scenario StaticThermalScenarioDescriptor thermal_scenario; thermal_scenario.materials = {{"Aluminum 6061-T6": material}}; thermal_scenario.boundary_conditions = {fixed_temp, convection}; thermal_scenario.internal_conditions = {constant_heat}; thermal_scenario.thermal_metadata.environment_temperature = 0.0; thermal_scenario.metadata.resolution = 10000; // Optional settings thermal_scenario.metadata.basis_order = 2; // 2 = quadratic elements thermal_scenario.metadata.solver_override = Intact::SolverType::AMGCL_amg; // iterative solver for thermal scenarios.
Finalize Simulation Setup and Execute
Stress Simulation is created using
StressSimulator. It takes the following inputs:An
assemblyor the list ofMaterialDomainsLinearElasticScenarioDescriptorthat describes the simulation scenario
// Initialize and run the linear elastic scenario Intact::StressSimulator simulator = StressSimulator(assembly, scenario); simulator.solve();
Modal Simulation is created using
ModalSimulator. It takes the following inputs:An
assemblyor the list ofMaterialDomainsModalScenarioDescriptorthat describes the simulation scenario
// Initialize and run the modal scenario Intact::ModalSimulator modal_simulator = ModalSimulator(assembly, modal_scenario); modal_simulator.solve();
Query and Result Output¶
Create a
QueryResultobject that specifies the domain to be sampled. It takes a singlecomponentor anassemblyas inputIntact::Assembly assembly = {component_1, component_2}; Intact::QueryResult results(component_1); // sample only the defined component Intact::QueryResult results(assembly); // sample on the full assembly
Specify a query class and type that defines what quantity you are querying. The query classes and types available are as follows :
Global Query is for querying quantities defined for the entire domain/structure.
For Modal Simulation, the only
GlobalQueryTypeisFrequency.For Stress Simulation, the following
GlobalQueryTypequeries are available:Complianceis a single value.TotalReactionForceis a tuple of dimension 3, representing the total reaction force.[Fx, Fy, Fz]
ReactionForceis a tuple of dimension 3 for each restrained boundary, in the order the boundary conditions were added to theLinearElasticScenarioDescriptor.[Fx, Fy, Fz]
TotalReactionMomentis 3 tuples of dimension 3, representing the moments about the origin generated by reaction forces. Using[r1, r2, r3]to represent the vector from the origin to the reaction force, and using[Fx, Fy, Fz]to represent the reaction force, the moments are:[0, r2 * Fx, r3 * Fx] [r1 * Fy, 0, r3 * Fy] [r1 * Fz, r2 * Fz, 0]
TotalAppliedForceis a tuple of dimension 3, representing the total applied load.[Fx, Fy, Fz]
TotalAppliedMomentis 3 tuples of dimension 3, representing the moments about the origin generated by the applied loads. Using[r1, r2, r3]to represent the vector from the origin to the applied load, and using[Fx, Fy, Fz]to represent the applied load, the moments are:[0, r2 * Fx, r3 * Fx] [r1 * Fy, 0, r3 * Fy] [r1 * Fz, r2 * Fz, 0]
// GlobalQuery example // Create a GlobalQuery to query the first mode of a modal simulation Intact::QueryResult results(assembly); Intact::GlobalQuery frequency_query(Intact::GlobalQueryType::Frequency, Intact::DiscreteIndex(0)); // Sample the simulation for the specified query auto freq_1 = simulator.sample(frequency_query, results); std::cout << freq_1.get(0, 0) << std::endl; // Print out the first mode in Hz // Example use to get all the modes // Note, the simulator would need this: // modal_scenario.modal_metadata.desired_eigenvalues = 10 for (auto i = 0; i < modal_scenario.metadata.desired_eigenvalues; i++) { // Create the query for the current mode Intact::GlobalQuery query(Intact::GlobalQueryType::Frequency, Intact::DiscreteIndex(i)); // Sample the query using the simulator auto r = simulator.sample(query, results); std::cout << r.get(0, 0) << std::endl; }
Field Query is for querying field quantities defined at any point in the domain. This depends on the physics type.
For Stress Simulation, the following
FieldTypeinputs are availableDisplacementtuple of dimension 3 for each point[x-displacement, y-displacement, z-displacement]
StrainandStressare each a tuple of dimension 6 for each point[stress_xx, stress_yy, stress_zz, stress_yz, stress_xz, stress_xy] [strain_xx, strain_yy, strain_zz, strain_yz, strain_xz, strain_xy]
TopologicalSensitivity,StrainEnergyDensity, andVonMisesStressare each a tuple of dimension 1 for each point
Field Query Interface usage
// FieldQuery example // Create a FieldQuery to query displacement Intact::QueryResult results(assembly); Intact::FieldQuery displacement_query(Intact::FieldType::Displacement); // Create a FieldQuery with optional input to query the y-component Intact::FieldQuery y_displacement_query(Intact::FieldType::Displacement, 1); // FieldQuery with optional input to query the norm of displacement Intact::FieldQuery displacement_magnitude_query(Intact::FieldType::Displacement, true); // Sample the simulation with the given query to create a VectorArray // * more info on VectorArrays are provided in the subsequent section * auto displacement_VectorArray1 = simulator.sample(displacement_query, results); auto displacement_VectorArray2 = simulator.sample(y_displacement_query, results); auto displacement_VectorArray3 = simulator.sample(displacement_magnitude_query, results); auto displacement1 = displacement_VectorArray1.get(i, j); // jth component of the displacement (0 = X, 1 = Y, or 2 = Z) at the ith sampling point auto displacement2 = displacement_VectorArray2.get(1, 0); // y-displacement value at the second sampling point auto displacement3 = displacement_VectorArray3.get(1, 0); // displacement magnitude at the second sampling point
For Modal Simulation, the only
FieldTypeavailable isDisplacement, which corresponds to the mode shape information and requires an index for the specified mode.// Create a field query for the displacement/mode shape of mode 1 auto mode_num = 0; // first mode Intact::FieldQuery modal_field_query(Intact::Field::Displacement, Intact::DiscreteIndex(mode_num))
Sample and Export Results¶
Sampling results in-memory
Methods to sample results of the simulation and store/print
VectorArrayresults from the queries created above.// Query results Intact::QueryResult results(assembly); Intact::FieldQuery stress_query(Intact::FieldType::Stress); // a field is needed to create a field query auto stress_VectorArray = simulator.sample(stress_query, results);
This sampling is stored in a
VectorArrayof sizen_tuplebydimension,n_tupleis the number of points sampled in the component/assembly and dimension depends on the query type. For example,FieldQuery(Intact::FieldType::Displacement)has a dimension of 3 for each displacement component, thusVectorArray.get(i, 2)would get the z-displacement of pointi.// Get the number of tuples (vectors) in the VectorArray (one per point results are sampled at) auto n_tuples = stress_VectorArray.n_tuples(); // Get the dimension of each vector - in this case 6, one value for each stress component auto dimension = stress_VectorArray.dimension(); auto stress_xx = stress_VectorArray.get(i, 0); // stress_xx at i-th sample point auto stress_yy = stress_VectorArray.get(i, 1); // stress_yy at i-th sample point auto stress_ij = stress_VectorArray.get(i, j); // jth stress component (0, 1, 2, 3, 4, or 5) of the ith tuple
Export results to a file: Once the query is created,
resultscan be used to write a file which contains all solution fields in VTK UnstructuredGrid format via theresults.writeVTKmethod which has two inputs:file name
"*.vtu"UnitSystemis an attribute in the*.vtu( Note that this argument is just metadata in the*.vtufile. The result magnitudes are in the unit of the scenario regardless of the unit system specified. )
// Write results to a file (unit system is saved as a metadata in the vtu file) Intact::QueryResult results(assembly); Intact::FieldQuery stress_query(Intact::FieldType::VonMisesStress); simulator.sample(stress_query, results); // Write results to a file (unit system is saved as a metadata in the vtu file) results.writeVTK("cantilever_beam_results.vtu", Intact::UnitSystem::MeterKilogramSecond);
Sampling on Custom Geometries¶
Another important functionality is the ability to specify a point set to sample on. This can be done by creating a new
sampling_componentconsisting of vertices at the desired sampling locations. Note that thesampling_componentis not to be included in the assembly that is being simulated.// Create an empty MeshModel to store vertices for desired sampling locations auto sampling_geometry = Intact::MeshModel(); // Add the desired sampling point locations and store their ID for later use auto test_index1 = sampling_geometry.addVertex({6.0, 0.0, 0.0}); auto test_index2 = sampling_geometry.addVertex({3.0, 0.0, 0.0}); auto sampling_component = Intact::MaterialDomain(sample_geometry, "material_name", scenario); // Define the assembly to be simulated (note that the sampling_component is not included) auto component = Intact::MaterialDomain(component_geometry, "material_name", scenario); Intact::Assembly assembly = {component}; Intact::StressSimulator simulator(assembly, scenario); simulator.solve(); Intact::FieldQuery displacement_query(Intact::Field::Displacement); Intact::QueryResult sampled_results(sampling_component) // sample only the custom point set auto sampled_VectorArray = simulator.sample(displacement_query, sampled_results); auto displacement_index1 = sampled_VectorArray.get(test_index1, 0); // x-displacement at above specified index1 auto displacement_index2 = sampled_VectorArray.get(test_index2, 1); // y-displacement at above specified index2
LevelOpt¶
LevelOpt is another
ScenarioDescriptor(LevelOptScenarioDescriptor) for level set structural topology optimization. It supports all of the standard linear elastic boundary conditions and a variety ofmetadataoptimization parameters.LevelOpt scenario is created using
LevelOptScenarioDescriptor. It shares the following inputs with otherScenarioDescriptorclasses:boundary_conditions. LevelOpt supports multiple load cases, which can be input to a single optimization scenario using uniqueload_case_id. This allows LevelOpt to consider each load individually rather than the net load.# multiple load case optimization needs unique load_case_ids auto fixed_boundary1 = std::make_shared<Intact::FixedBoundaryDescriptor>(); fixed_boundary1->boundary = Intact::MeshModel("fixed.ply"); fixed_boundary1->load_case_id = 0; auto fixed_boundary2 = std::make_shared<Intact::FixedBoundaryDescriptor>(); fixed_boundary2->boundary = Intact::MeshModel("fixed.ply"); fixed_boundary2->load_case_id = 1; auto load1 = std::make_shared<Intact::VectorForceDescriptor>(); load1->boundary = Intact::MeshModel("load1.ply"); load1->direction = {1, 0, 0}; load1->magnitude = 1000; load1->load_case_id = 0; auto load2 = std::make_shared<Intact::VectorForceDescriptor>(); load2->boundary = Intact::MeshModel("load1.ply"); load2->direction = {1, 0, 0}; load2->magnitude = 1000; load2->load_case_id = 1; auto load_cases = {fixed_boundary1, load1, fixed_boundary2, load2};
internal_conditionsresolutionorcell_sizeunitssolver_typeused in the initial linear elastic simulation with the following options:MKL_PardisoLDLT(default) direct solverAMGCL_amg_rigid_bodyiterative solver
basis_orderused in the initial linear elastic simulation
LevelOpt Metadata Settings¶
The set of
metadataparameters specific to theLevelOptScenarioDescriptorinclude:vol_frac_cons(volume fraction constraint) sets the target volume of the final design as a fraction of the initial volume.voxelSize, or level set cell size, determines the size of the level set grid cells as a fraction of the FEA grid cell size.move_limitcontrols the extent of changes per optimization step, as a factor of thevoxelSize.opt_max_iter(optimization max iterations) sets the maximum number of iterations for the optimization process. Each iteration refines the design by updating the topology based on the objective function and constraints.fix_thicknessspecifies the region around boundary conditions that remains unchanged as a factor of level set grid cell size.smooth_iterdefines the frequency the geometry is smoothed during the optimization process as a number of iterations.enable_fixed_interfacesallows specifying if the interface between the design domain (optimized) and non-design domain should be fully preserved.Truepreserves the interface andFalseallows material to be removed at the interface.num_load_casesis a input required for an optimization scenario with multipleload_case_id. This enables individual load cases to be considered separately during optimization instead of a net load.output_directoryis an optional input that specifies an output directory to write per-iteration optimization results. The results that are written per-iteration are the design written as a PLY file, a CSV file namediteration_history.txtthat contains the iteration number, the load case number, the compliance and the volume fraction of the design.
// Setup the LevelOpt optimization scenario descriptor Intact::LevelOptScenarioDescriptor leveloptscenario; // Standard scenario parameters leveloptscenario.materials = {{"Aluminum": material}}; leveloptscenario.metadata.cell_size = 2.5; leveloptscenario.metadata.units = Intact::UnitSystem::MeterKilogramSecond; leveloptscenario.metadata.solver_override = Intact::SolverType::MKL_PardisoLDLT; // direct LinearElastic solver leveloptscenario.metadata.basis_order = 1; // linear order for LinearElastic solver leveloptscenario.boundary_conditions = load_cases; // consist of two sets of load cases // LevelOpt specific metadata leveloptscenario.optimization_metadata.vol_frac_cons = 0.2; // 20% target volume leveloptscenario.optimization_metadata.voxelSize = 0.5; // 0.5 (default) level set cell size factor leveloptscenario.optimization_metadata.move_limit = 1.0; // 1.0 (default) move limit factor leveloptscenario.optimization_metadata.opt_max_iter = 10; // 10 design iterations leveloptscenario.optimization_metadata.fix_thickness = 4; // 4 (default) level set cells which are unchanged near BCs leveloptscenario.optimization_metadata.smooth_iter = 1; // smoothing performed at every 1 iteration leveloptscenario.optimization_metadata.enable_fixed_interfaces = true; // retain full contact between assembly components leveloptscenario.optimization_metadata.num_load_cases = 2; // 2 load cases created
LevelOpt Optimization and Supported Queries¶
To run an optimization scenario a design domain
Material Domainmust first be defined. For assemblies, additional non-designMaterial Domain(s)need to be defined. Note, the design domainMeshModelrequires a uniqueinstance_id.// make sure to include instance_id for design_geometry/design_domain auto design_geometry = Intact::MeshModel("design_domain.stl"); design_geometry.instance_id = "ex_design_domain"; // can be any unique id/name design_geometry.refine(); // Create material domains and assembly auto design_domain = Intact::MaterialDomain(design_geometry, "Aluminum", leveloptscenario); component1 = Intact::MaterialDomain(body1, "Aluminum", leveloptscenario); component2 = Intact::MaterialDomain(body2, "Aluminum", leveloptscenario); Intact::Assembly assembly = {design_domain, component1, component2};
The
LevelOptoptimization solver then takes the following arguments:design
Material Domainassembly or list of all design and non-design
Material Domain(s)LevelOptScenarioDescriptorwhich describes the optimization scenario parameters and inputs.starting design
MeshModel, or if no starting design is used, anullptrargument.
// Create and run the simulation auto optimizer = Intact::LevelOpt(design_domain, assembly, leveloptscenario, nullptr); optimizer.optimize(); // Or, create and run the simulation with optional starting design auto starting_design = Intact::MeshModel("starting_design.ply"); optimizer = Intact::LevelOpt(design_domain, assembly, leveloptscenario, starting_design); optimizer.optimize();
LevelOpt Queries include support for two
GlobalQueryTypeclasses,ComplianceandVolumeFractionand twoFieldQueryclasses,BoundarySensitivityandBoundaryVelocity. A discrete index argument corresponding to the optimization iteration is required to query for any of the previously described quantities.// LevelOpt global queries Intact::GlobalQuery compliance_query = Intact::GlobalQuery(Intact::GlobalQueryType::Compliance, Intact::DiscreteIndex(iteration)); Intact::GlobalQuery volume_fraction_query = Intact::GlobalQuery(Intact::GlobalQueryType::VolumeFraction, Intact::DiscreteIndex(iteration)); auto compliance = optimizer.sample(compliance_query); auto volume_fraction = optimizer.sample(volume_fraction_query); double compliance_value = compliance.get(0,0); double volume_fraction_value = volume_fraction.get(0,0); // LevelOpt field queries auto boundary_sensitivity_query = Intact::FieldQuery(Intact::Field::BoundarySensitivity, Intact::DiscreteIndex(0)); auto boundary_velocity_query = Intact::FieldQuery(Intact::Field::BoundaryVelocity, Intact::DiscreteIndex(0)); // no QueryResult() object, because boundary sensitivity is only defined on design boundary auto r_s = optimizer.sample(boundary_sensitivity_query); // no QueryResult() object, because boundary velocity is only defined on design boundary auto r_v = optimizer.sample(boundary_velocity_query); double sensitivity_value = r_s.get(0,0) // tuple of dimension 1 for each point double velocity_value = r_v.get(0,0) // tuple of dimension 1 for each point
Output mesh designs can be stored using
getDesigns()from the LevelOpt scenario optimization.
// run LevelOpt Scenario
auto optimizer = LevelOpt(design_domain, assembly, leveloptscenario, nullptr);
optimizer.optimize();
// get the design iterations from the optimization scenario
auto designs = optimizer.getDesigns();
Example Files¶
Stress, Thermal, Modal¶
Complete examples of performing a structural simulation a modal simulation, or a static thermal simulation are available, as well as the required geometry files: beam geometry, restraint geometry, load geometry.
LevelOpt¶
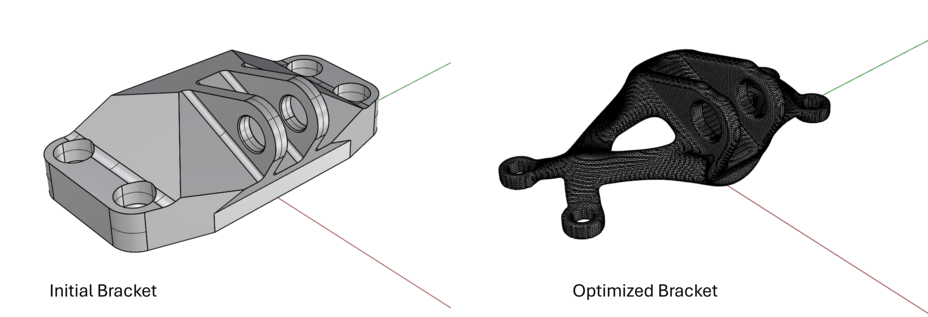
GE Bracket Example¶
A complete example of performing a LevelOpt bracket optimization is available along with all geometry files: bracket geometry, restraint, load1, load2, and a reference starting design.
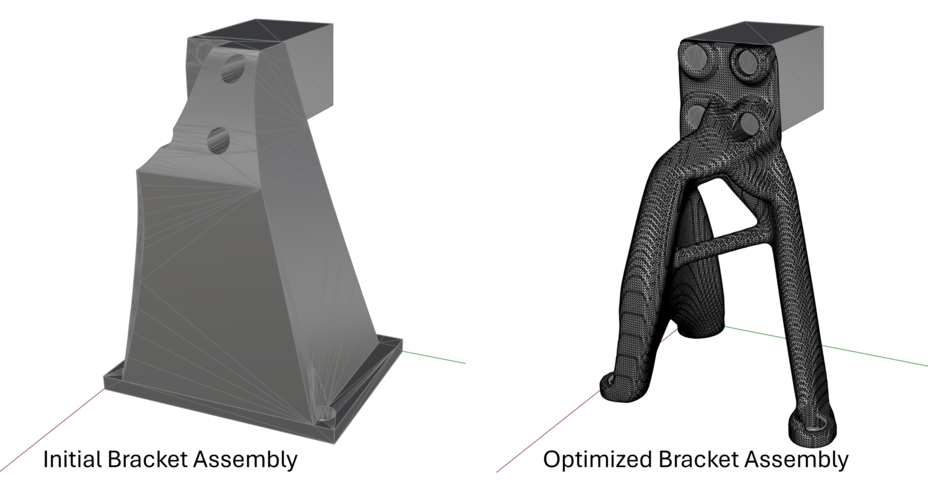
NASA Bracket Assembly Example¶
A complete example of performing a LevelOpt bracket assembly optimization is available along with all geometry files: design geometry, non-design geometry, restraint, load, and a reference starting design.
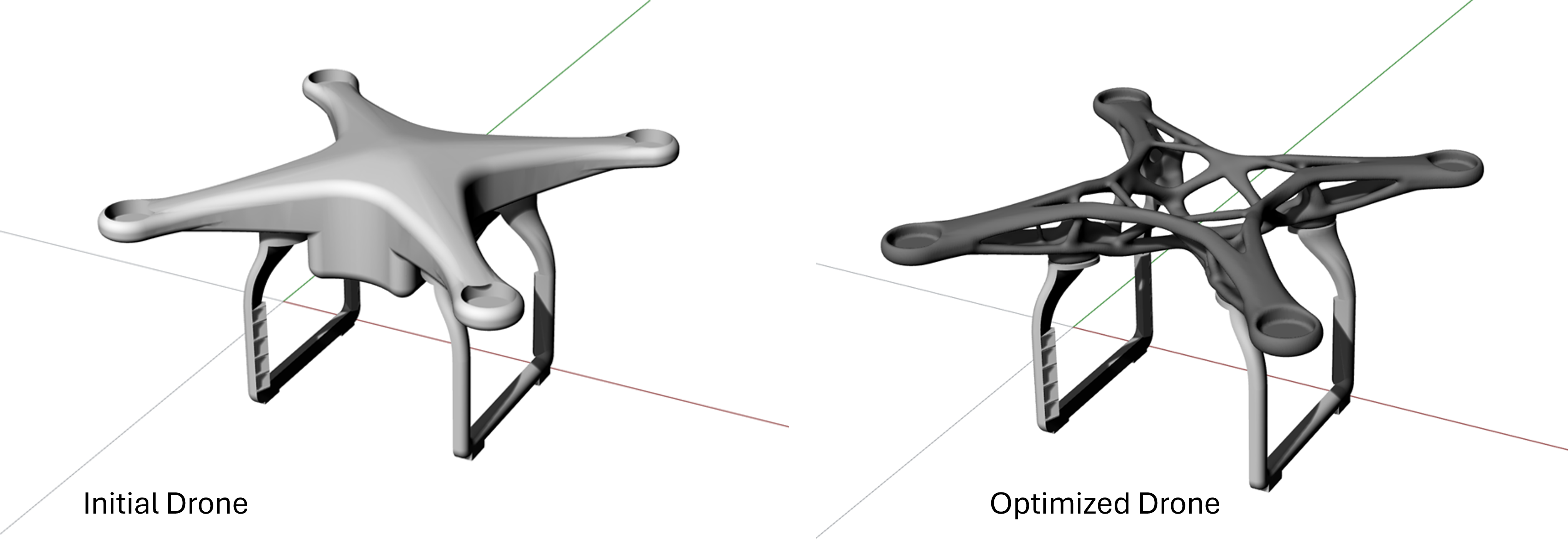
Multiple Load Case Drone Example¶
A complete example of performing a LevelOpt bracket assembly optimization is available along with all geometry files: design geometry, non-design leg1 geometry, non-design leg2 geometry, restraint1, restraint2, loads, and a reference starting design.